Libra & basket currencies fluctuations from 1999 to 2019

General · 23 Sep 2019

[Currency exchanges rates used for this article are published daily by the European Central Bank. They can be shared: send us an email at chaingrok@gmail.com]

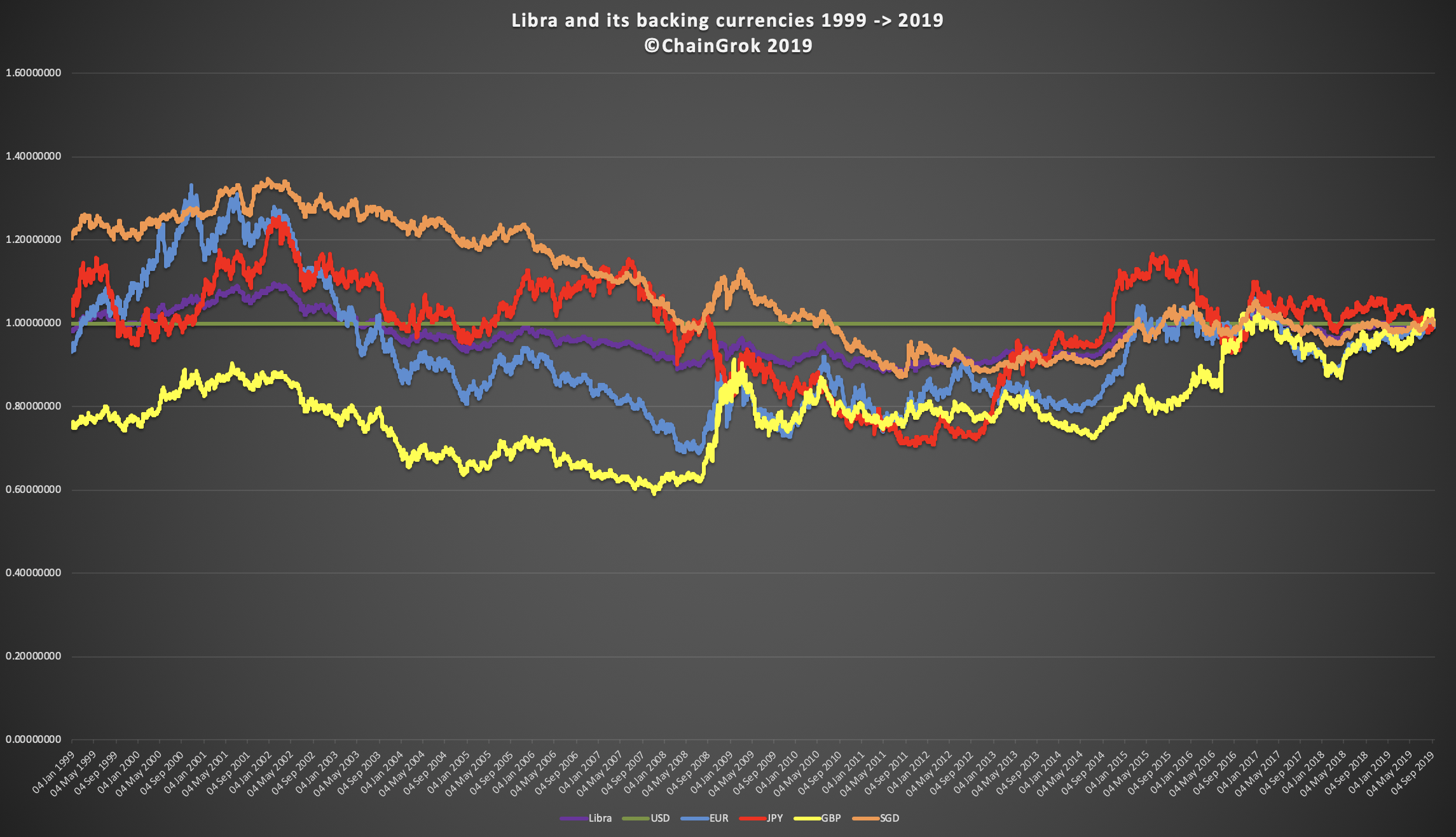Figure 1 - Libra and basket currencies versus USD: 1999 -> 2019 (right click > View image in your browser to enlarge)

The German newspaper Der Spiegel just reported the structure chosen by the Libra Association for the fiat currency basket underlying its eponymous stablecoin:

US dollar (USD): 50%
Euro (EUR): 18%
British Pound (GBP): 14%
Japanese Yen (JPY): 11%
Singaporean Dollar (SGD): 7%

Libra wants to be a stablecoin: as per Wikipedia "Stablecoins are cryptocurrencies designed to minimize the volatility of the price of the stablecoin , relative to some "stable" asset or basket of assets. A stablecoin can be pegged to a cryptocurrency, fiat money, or to exchange-traded commodities (such as precious metals or industrial metals). Stablecoins redeemable in currency, commodities, or fiat money are said to be backed, whereas those tied to an algorithm are referred to as seigniorage-style (not backed)."

Regarding stablecoins, the Libra Association pushes the envelope: the most famous and successful fiat-based ones like Tether, USDC, Gemini Dollar are based on a single currency, most often the US Dollar, while Libra's basket is composed of five of them.

Why so? Probably because Libra wants to be:

Global: you cannot aim to be used worldwide if you rely on one single currency. Trust for a currency-based stablecoin will build more easily by end-users if they see their home currency represented.
Neutral: similarly, you cannot be deemed as neutral if you put all your eggs in one single monetary basket and get consequently directly bound to the decisions of the corresponding central bank.
Independent: the links to several currencies rather than a single one are supposed to better isolate the stablecoin from political choices, and the corresponding fluctuations, of one single asset.

But, more importantly, by mixing several fiat currencies in its underlying basket, the Libra Association tries to achieve the mathematical stability fostered by the purpose of its cryptocurrency: averaging over several rock-solid, large-scale and well trusted fiat currencies should reduce the valuation "bumps".

Indeed, the financial structure of Libra is based on the same principles as the Special Drawing Rights (SDR) of the International Monetary Fund (IMF). The SDR is a unit of account rater than a currency per se. The shares in the SDR basket are structured in the following manner:

US dollar: 41.73%
Euro: 30.93%
Chinese Yuan: 10.92%
Japanese Yen: 8.33%
British Pound: 8.09%

It is interesting to note that the only difference in the choice of the fiats is the Chinese Yuan replaced by the Singaporean Dollar. Due to the current race between China and Facebook around cryptocurrencies?

Anyway, those multi-currency tokens like Libra or SDR do, by design, fluctuate over time. SDR was not aimed at being a stablecoin but rather at being a mirror of economical activity. So, its stability is not of primary importance.

But, for Libra as a stablecoin, the challenge may be different: its designers probably want it to be as stable as possible over long period of time so that trust can build, and usage can grow. Nobody wants for usual goods to have today a price very different from what it was yesterday!

So, in Figure 1 above, to see what the future could look like based on history, for each currency in the Libra basket, we've taken its exchange rate to the US dollar (as worldwide leading and reference currency), as published by the European Central Bank (ECB) since 1999 to see how this design satisfies the stability purpose. This chart represents the relative value of the depicted currencies to the USD, taking the current exchange rate as of Sept 23, 2019 as 100% for each of them. The historical value of Libra is computed based on the weighted sum corresponding to its structure. See final section Computation for details on the formula. It may seem unusual to take reference today and then go back in time,but we believe that it makes analysis easier in this specific situation.

The table 2 below reports the maximum and minimum values to the dollar over those 20 years compared to their value of September, 23rd 2019:

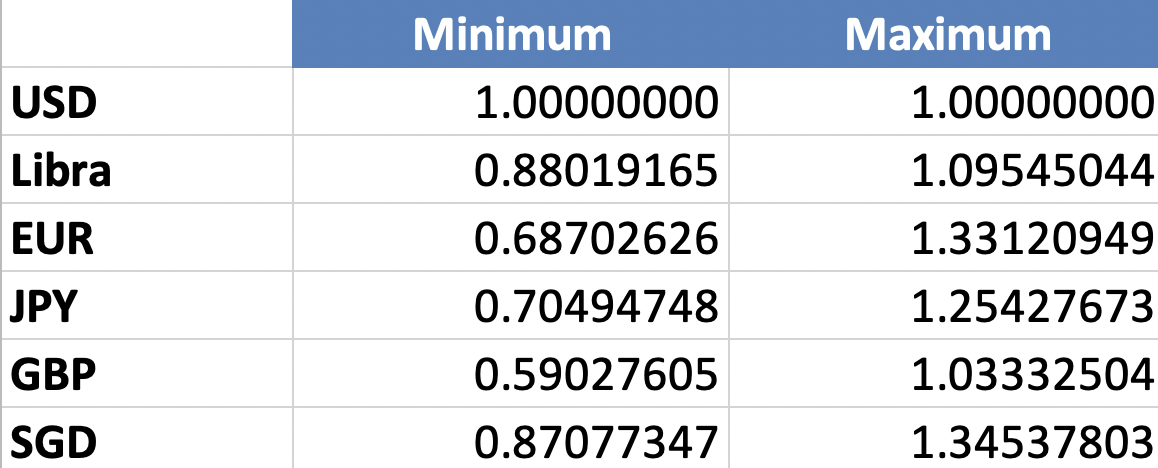Table 2 - Libra and basket currencies up/down peaks versus USD: 1999 -> 2019

Some conclusions that can be extracted from these chart and table:

Over the last 20 years, the currencies over which Libra is announced to be based fluctuate quite significantly. Deltas of 40% over the dollar in constant value (100% being today) has been the minimum.
If we take the US dollar as the worldwide reference due to its global weight, Libra performs better in terms of stabilized value than any of the currencies in its basket with less than 25% of fluctuation while the fiats have deltas over 40%. In that sense, it would achieve its goal of better stability than single-asset cryptocurrencies.

Based on those historical numbers, the theoretical conclusions above bring some interesting operational questions for the Libra Association:

Will the price of Libra on authorized exchanges be forced by the Association to reflect those fluctuations when an end-user executes trades between Libras and its native fiat currency?
Will the Libra Association redefine the basket structure with different structure, i.e. different percentages or different currencies / assets, over time if stability is damaged by too vivid fluctuations of some components?
Will they rebalance – in quasi real time - the effective fiat assets in the Libra Reserve if activities of end-users, i.e. trades of Libra against Fiat, tend to jeopardize the official structure toward a radically different composition, and consequently a different value of the Libra currency?
If not, will the Libra Association give access – again in quasi real time – to third parties allowed to develop some arbitrage business in order to bring the current situation of the Reserve as close as possible to its theoretical composition?
Will the regulators, especially the ones of Switzerland where the headquarters of the Libra Association are located and also those of the countries where Libra will be used, enforce some rules to deal one way or another with the points above, some of them to be potentially perceived as issues by those regulators?

But the ultimate question is probably the following: will those fluctuations look acceptable to the potential user community (consumers, businesses, etc.) in order to build trust in this new currency and build a wide-scale and sustainable ecosystem on the long term?

The effective "birth" of Libra is still somewhat remote, and many details of its exact shape remain to be negotiated with authorities and then be discussed / accepted in the upcoming Libra community. So, the months to come will deliver answers to those questions.

If our analysis inspires you for remarks or additional questions, the comment section below is wide open for this purpose!

Computation

The curves in Figure 1 are based on a static situation allowing a better understanding of the fluctuations: 10 members of the Libra Association bring their 10 millions USD contribution as required by the Libra whitepaper. 6 of them bring this amount in Euros while 4 of them bring it in British Pounds. It will make the equations simpler to write since this simplified Libra has only 2 currencies in its basket : 60% EUR and 40% GBP both priced in USD over time as it is our reference fiat currency.

This fixed basket is (much) simpler than the reality will be: it doesn’t take into account end-user activity (consumers acquiring / redeeming Libras), partner activity (partners entering / leaving the association), trading activity (reserve funds invested in government bonds). Anyway, let’s mathematically describe how the value of this simplified basket evolve:

1) Let’s call Vt0(Libra) the initial value of the Libra Reserve at time t0 in the reference currency (USD here). So,

Vt0(Libra) = Vt0(EUR) + Vt0(GBP)

with Vt0(EUR) = Vt0(Libra) * r(EUR) where r(EUR) represents the ratio of EUR in the basket: 0.6 in our case
     Vt0(GBP) = Vt0(Libra) * r(GBP) where r(GBP) = 0.4 in our case

2) Then, QtO(EUR) represents the quantity of EUR at tO and QtO(GBP) represents the quantity of GBP at tO. So,

Qt0(EUR) = Vt0(EUR)/Ct0(EUR) where Ct0(EUR) represents the cost (i.e. exchange rate) of EUR in reference currency (USD in our case)
Qt0(GBP) = Vt0(GBP)/Ct0(GBP) where Ct0(GBP) represents the cost of GBP in reference currency (USD in our case)

3) Consequently,

Vt0(Libra) = Ct0(EUR)*Qt0(EUR) + Ct0(GBP)*Qt0(GBP)

4) Let’s now find the fluctuation of the value of the Libra Reserve at new time t1 as quantities remain invariant:

         Vt1(Libra) = Ct1(EUR)*Qt0(EUR) + Ct1(GBP)*Qt0(GBP)
                    = Ct1(EUR)*(Vt0(EUR)/Ct0(EUR)) + Ct1(GBP)*(Vt0(GRP)/Ct0(GBP))
                    = Ct1(EUR)*((Vt0(Libra)*r(EUR))/Ct0(EUR)) + Ct1(GBP)*((Vt0(Libra)*r(GBP))/Ct0(GBP))
                    = Vt0(Libra) * ((r(EUR) * Ct1(EUR)/Ct0(EUR) + r(GBP) * Ct1(GBP)/Ct0(GBP))

So, at any given moment in time, the value of the Libra Reserve is its initial value multiplied by the weighted sum of the price (i.e. exchange rate) between current time and reference time. The weights are the ratios defined during the design of the basket.

The example above has been computed with 2 fiat currencies in the basket but, to come back to real situation, the formula above extends to all the currencies of the official Libra basket as

Vt1(Libra) = Vt0(Libra) 
               * (r(USD) * Ct1(USD)/Ct0(USD) 
                  + r(EUR) * Ct1(EUR)/Ct0(EUR) 
                  + r(GBP) * Ct1(GBP)/Ct0(GBP)
                  + r(JPY) * Ct1(JPY)/Ct0(JPY)
                  + r(SGD) * Ct1(SGD)/Ct0(SGD)
                  )

with r(USD)= 0.5, r(EUR)=0.18, r(GBP)=0.14, r(JPY)=0.11, r(SGD)=0.07. Of course, Ct0(USD) = Ct1(USD) = Ctn(USD) = 1 as the dollar is chosen as reference here.

This final formula is the one applied in the creation of Figure 1 and in the extraction of the numbers in Table 2 with t0 being September, 23rd 2019.